알고리즘 [ Algorithm ]

[ Algorithm ]

---

1. 선택정렬 Selection Sort

 

∘ 해당 순서에 원소를 넣을 위치를 정해놓고 원소를 선택하는 알고리즘

∘ 자리를 선택하고 그 자리에 오는 값을 찾는 것

∘ 불안정 정렬

∘ 비교 횟수 : (n-1) + (n-2) + ... + 2 + 1 ⇨ n(n-1)/2

∘ 시간복잡도 : O(n^2)

for( int i=0; i<n-1; i++)
      for(int j=i+1; j<n; j++)
         if( arr[i] > arr[j] ) swap(arr[i], arr[j]);
      }
}

 

---

2. 거품정렬 Bubble Sort

 

∘ 인접한 두 원소를 비교하고 자리를 교환하는 알고리즘

∘ 안정 정렬

∘ 비교 횟수 : (n-1) + (n-2) + ... + 2 + 1 ⇨ n(n-1)/2

∘ 시간복잡도 : O(n^2)

 

for( int i=0; i<n-1; i++) {
    for(int j=1; j<n-i; j++) {
      if( arr[j] < arr[j-1] ) swap(arr[j-1], arr[j]);
    }
}

---

3. 삽입정렬 Insertion Sort

 

∘ 손 안의 카드를 정렬하는 방법과 유사

∘ 새로운 원소를 기존 정렬된 원소들 사이에 자리를 찾아 삽입하는 방식

∘ 안정 정렬

∘ 최선 : 모두 정렬되어 있는경우 O(N)

∘ 최악 : 역순으로 정렬되어 있는 경우 O(N^2)

 

for(int i=1; i<n; i++) {
	
    int target = arr[i];
    int j = i-1;
    
    while(j >= 0 && target < arr[j]) {
    	arr[j+1] = arr[j];
        j--;
    }
    arr[j+1] = target;
}

 

---

4. 병합정렬 Merge Sort

 

∘ 분할 정복 방법으로 통해 구현

∘ 1/2씩 분할하다가 원소가 하나의 배열이 될 때부터 병합해나가며 비교+정렬

∘ 영역으로 쪼갬(mergeSort) → 정렬(merge)

∘ 평균, 최선, 최악 모두 O(nLogN)

∘ 안정 정렬

 

private int[] arr, tmp;
private int n = 9;

public static void main(String[] args) { 
	arr = new int[]{1, 9, 8, 5, 4, 2, 3, 7, 6};
    tmp = new int[n]; 
    mergeSort(0, n-1); 
} 

public static void mergeSort(int start, int end) { 
	if (start<end) { 
    	int mid = (start+end) / 2; 
        mergeSort(start, mid); 
        mergeSort(mid+1, end); 
        
        int p = start; 
        int q = mid + 1; 
        int idx = p; 
        
        while (p<=mid || q<=end) { 
        	if (q>end || (p<=mid && arr[p] < arr[q])) tmp[idx++] = arr[p++]; 
            else tmp[idx++] = arr[q++];  
        }
        
        for (int i=start ; i<=end ; i++) { 
        	arr[i] = tmp[i]; 
        } 
    } 
}

---

5. 퀵정렬 Quick Sort

 

∘ 불안정 정렬

∘ Logic

    ⅰ 배열 가운데서 원소를 고름 (pivot)

    ⅱ. pivot 기준으로 배열을 나누고 왼쪽에 작은 값, 오른쪽에 큰값이 오게 한다.

    ⅲ. 분할된 두개의 배열에 대해 이 과정을 재귀적으로 반복

∘ 최선 : O(nLogN)

∘ 최악 : pivot이 항상 배열 내에서 최솟값/최댓값으로 설정될 경우 O(n^2)

∘ 평균적으로 가장 빠른 알고리즘

 

 

---

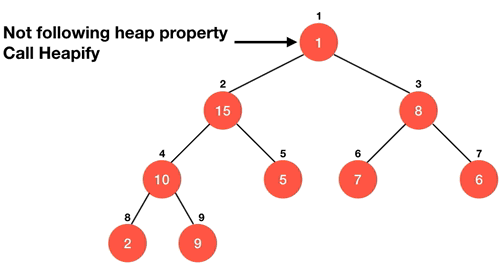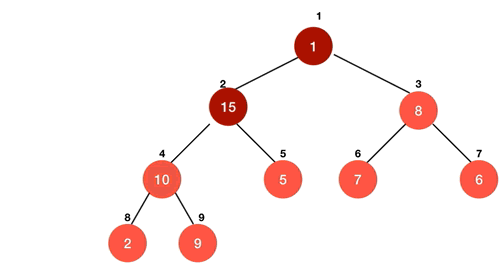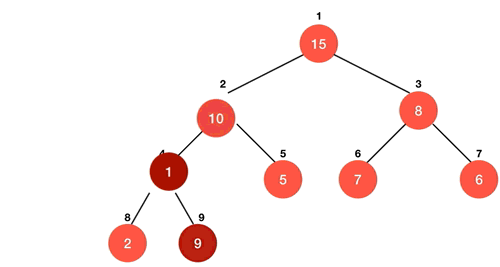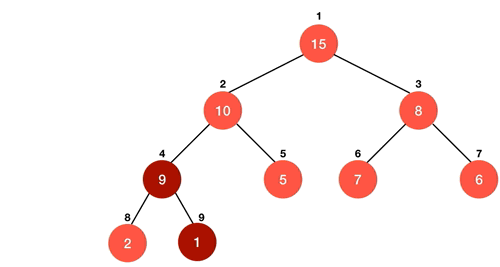
6. 힙 정렬 Heap Sort

 

∘ 완전 이진 트리를 기본으로 하는 힙 자료구조를 기반으로 한 정렬방식

∘ 불안정 정렬

∘ Logic

    ⅰ 최대 힙 구성(heapify) : O(logN)

    ⅱ. 루트의 값을 마지막 요소와 바꾼 후 힙 사이즈 –= 1 : O(1)

    ⅲ. 위의 과정을 반복 : O(N)

∘ 평균, 최선, 최악 : O(nLogN)

 

 

---

 

7. 투포인터 알고리즘 ( 슬라이딩 윈도우 )

 

∘ 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가며 원하는 결과를 얻는 알고리즘

∘ O(N+N) => O(N)

 

 

---

8. BFS

∘ 너비 우선 탐색, queue 사용

∘ 최소비용을 찾는 문제에 적합

∘ 인접행렬 : O(V^2), 인접리스트 : O(V+E)

---

9. DFS

∘ 깊이 우선 탐색 ,재귀 이용

∘ 모든 경로를 방문해야 할 경우에 적합

∘ 인접행렬 : O(V^2), 인접리스트 : O(V+E)

---

10. 이분탐색

∘ 탐색 범위를 두 부분으로 분할하면서 찾는 방식

∘ O(LogN)

// boolean function(int mid) : mid 값이 결과로 적합한 지 판단

int left = MIN, right = MAX;
int result = 1;
while (left <= right) {
    int mid = (left + right) / 2;
    if (function(mid)) left = mid + 1;
    else {
        result = mid;
        right = mid - 1;
    }
}

---

11. 유클리드 알고리즘

∘ X % Y = R일때 X,Y의 최대공약수는 Y,R의 최대공약수와도 같다

∘ R이 0이 될 때의 Y가 X,Y의 최대공약수

 

∘ GCD ( 최대공약수 )

// 반복문
int gcd1(int a, int b) {
	int l;
	if(a < b) swap(a, b);
    
    while(b != 0) {
    	l = a % b;
        a = b;
        b = l;
    }
    return l;
}

// 재귀
int gcd2(int a, int b) {
	if(b==0) return a;
    return gcd(b, a%b);
}

---

12. LRU cache

∘ 캐시 : 데이터나 값을 미리 복사해놓은 임시 장소

∘ Doubly Linked List로 구현

---

13. DP

∘ 복잡한 문제를 간단한 여러 개의 하위 문제로 나누어 푸는 방식

∘ top-down (memoization) : 재귀를 이용하여 미리 dp[ ] 에 값 저장하며 내려옴

∘ bottom-up : 하위문제들로 상위 문제의 최적해를 구하는 방식

---

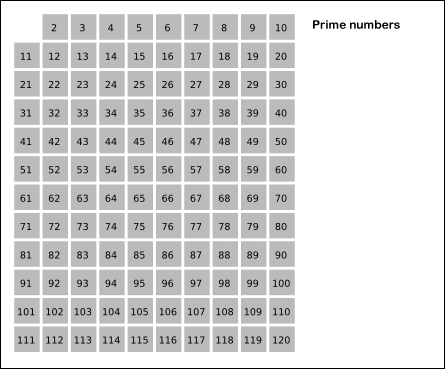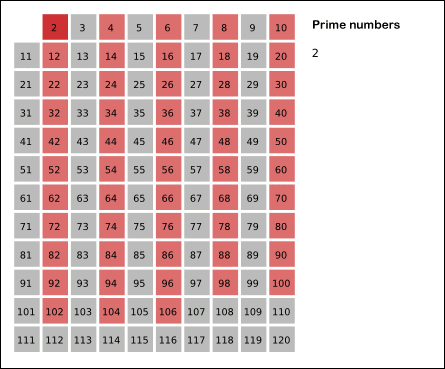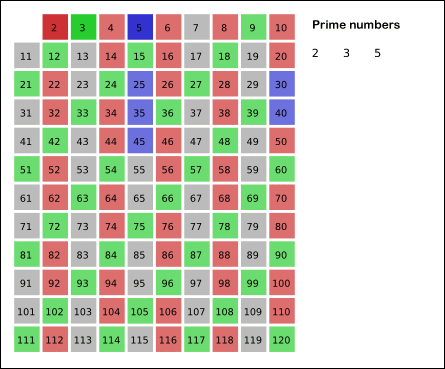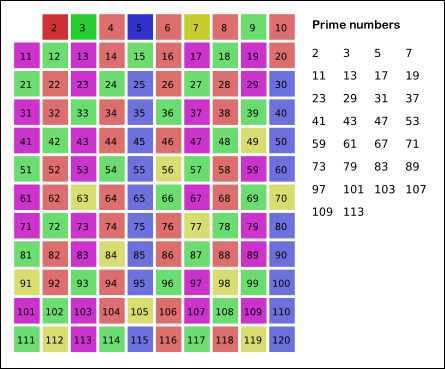
14. 에라토스테네스의 체

∘ 임이의 자연수에 대하여 그 자연수 이하의 소수를 모두 찾아주는 방법

∘ 1 부터 N 까지 늘려가면서 소수를 제외한 소수의 배수를 전부 지워가는 방법

public static void main(String[] args) {
    int N = 1000000;
    prime[0] = prime[1] = true;

    for(int i=2; i*i<=N; i++){
        if(!prime[i]){
            for(int j=i*i; j<=N; j+=i) prime[j]=true;                
        }        
    }    
}

---